Magnetic resonance enterography (MRE) is rapidly becoming the first-line imaging tool for evaluating the small bowel in patients with Crohn's disease. It can demonstrate mural and extramural complications, and the high contrast resolution, multiplanar capability, cine-imaging, and lack of ionizing radiation make it ideal for prolonged follow-up, according to radiologists from a top London hospital.
"A key question in the management of such patients is the assessment of disease activity," noted Dr. Nyree Griffin, consultant gastrointestinal radiologist at Guy's and St Thomas' National Health Service (NHS) foundation trust in London. "Clinical indices, endoscopic, and histological findings have traditionally been used as surrogate markers but all have limitations. MRE can help address this question."
MRE can distinguish between inflammatory, stricturing and penetrating disease, and can be performed prior to video capsule endoscopy (VCE) in excluding strictures where VCE can then be used to detect subtle mucosal disease. In combination with blood and fecal biomarkers and endoscopy, MRE can assist the treating clinician in distinguishing between inflammatory stenoses amenable to medical therapy and fibrostenotic disease requiring surgery, she wrote in an article published online on 16 March by Insights into Imaging.
T2-weighted, postcontrast and diffusion-weighted imaging (DWI) can be used. The value of DWI remains to be defined, but it may well have an adjunctive role in the assessment of disease activity and response evaluation.
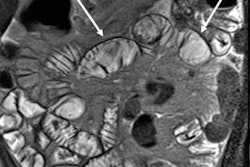
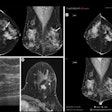
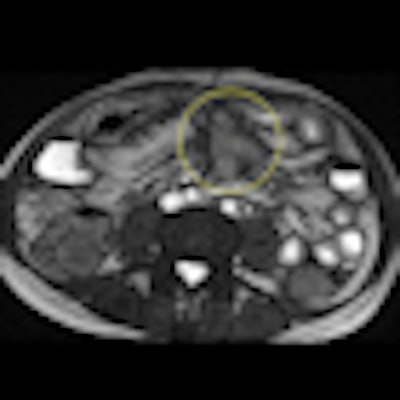
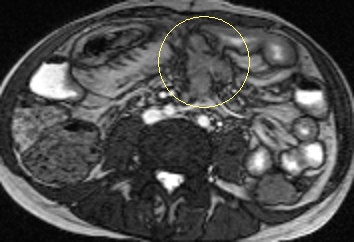 Axial true fast imaging with steady-state precession (FISP) image shows complications of penetrating Crohn's disease. There are multiple thickened loops of small bowel anteriorly in the abdomen with prominence of the vascular arcades. One loop in the left side of the abdomen shows local perforation with abscess collection within the mesentery (circle). All images courtesy of Dr. Nyree Griffin.
Axial true fast imaging with steady-state precession (FISP) image shows complications of penetrating Crohn's disease. There are multiple thickened loops of small bowel anteriorly in the abdomen with prominence of the vascular arcades. One loop in the left side of the abdomen shows local perforation with abscess collection within the mesentery (circle). All images courtesy of Dr. Nyree Griffin.In 2010, the European Crohn's and Colitis Organization (ECCO) gave new advice on the diagnosis and management of Crohn's disease. ECCO recommends either CT or MRE/MR enteroclysis as the current standards for assessing the small intestine due to their high diagnostic accuracy, and says radiation exposure should be considered when selecting techniques. MRE can help to categorize the relative components of inflammatory, penetrating or stricturing disease in each individual patient, and it is an ideal investigation for repeat bowel imaging in patients with Crohn disease, ECCO said.
At Guy's and St Thomas', patients fast for between four and six hours prior to the MRE study. In adults, oral contrast consists of at least 1-1.5 l of a 2.5% mannitol solution mixed with 0.2% carob bean gum. This solution acts as a hyperosmolar agent to draw fluid into the bowel, Griffin wrote. Mannitol is a biphasic agent that appears as low signal intensity on T1-weighted images and high signal intensity on T2-weighted images. The patient drinks the oral contrast agent at regular intervals over a period of about 40 minutes prior to the study. The patient is imaged on a 1.5-tesla MRI scanner (Siemens Healthcare), using a phased array surface coil, either in the supine or prone position (if no stoma is present).
"Coronal sequences are quicker to perform in the prone position, as there is a thinner volume of tissue to image," she stated. "Although prone imaging has been shown to result in better small bowel distension, both positions are equivalent with respect to lesion detection and characterization of changes in the bowel wall in Crohn's disease. With the exception of the cine and diffusion-weighted sequences, all scans are breath-hold and carried out in both the axial and coronal planes."
Diffusion-weighted imaging (DWI) has recently been added to the London hospital's MRE protocol. Three b values (b = 0, 100, and 800) are used, with axial images through the upper and lower abdomen obtained. The purpose of this is to help identify actively inflamed loops of bowel by the presence of restricted diffusion within the affected bowel wall, she elaborated.
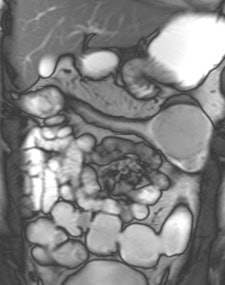
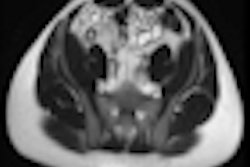
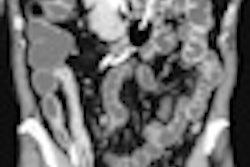
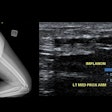
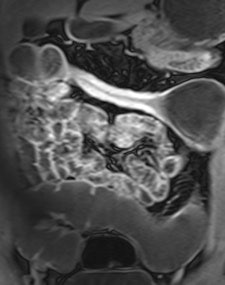 Example of predominantly fibrostenotic disease. Coronal true FISP (Left) and coronal T1 fat-saturated (Right) postcontrast images shows long stricture in the transverse colon with fibrofatty proliferation in the adjacent mesentery. There is dilatation distal to this stricture secondary to a further stricture in the descending colon (not shown).
Example of predominantly fibrostenotic disease. Coronal true FISP (Left) and coronal T1 fat-saturated (Right) postcontrast images shows long stricture in the transverse colon with fibrofatty proliferation in the adjacent mesentery. There is dilatation distal to this stricture secondary to a further stricture in the descending colon (not shown).MRE is a particularly useful in the assessment of treatment response. When MRI is performed during an acute relapse and then in remission, a reduction in both mural contrast enhancement and in mural thickness in affected segments is seen, but luminal stenosis may persist. Biologics such as infliximab and adalimumab have been used to treat patients with Crohn's disease resistant to other therapies with mucosal healing as a key treatment goal.
"From our experience, MRE can be used to show a significant reduction in inflammatory activity (as demonstrated by reduced mural thickening, edema, and enhancement) following treatment with such agents. DWI may have a role in response assessment with a predicted decrease in the degree of restricted diffusion. However, as yet there are no published papers on this subject," explained Griffin.
In a multidisciplinary team meeting involving the radiologist, gastroenterologist, histopathologist, and surgeon, she suggests that these important questions are addressed on MRE: extent of small and large bowel involvement at first presentation; distinction between active inflammatory and fibrotic stricturing disease; recognition of penetrating disease with the development of extramural complications; evaluation of response to medical therapy; and detection of recurrent disease following surgery.
The table shows the advantages and disadvantages of eachtechnique when compared with MRE.
Comparison of imaging modalities in the evaluation of Crohn's disease
|