The irradiation of healthy tissues during radiotherapy has been reduced substantially in recent years with the development of automated treatment planning techniques that shape the radiation beam to fit imaging data on tumor volume and location. Respiratory motion compensation algorithms, which compensate for the patient's breathing during treatment, are also playing a role.
Current methods of predicting breathing are cumbersome, however, and the task is technically daunting. Without compensation of breathing motion, the dose applied to the target lesion may be compromised. If the margin around the target is too large, significant amounts of healthy tissue may be irradiated.
The three-dimensional nature and variability of respiratory motion are additional complicating factors. Organs in the thorax and abdomen can move as much as 40 mm, and in three dimensions, during the breathing cycle. Patients move, cough, and breathe unevenly. Faster and more efficient algorithms will be needed to support a new generation of motion-tracking systems, which move the radiation beam in response to patient movement.
At the 2008 Computer Assisted Radiology and Surgery (CARS) meeting in Barcelona, Spain, Floris Ernst from the University of Luebeck in Germany discussed a new family of linear algorithms his group developed. The techniques yield comparable accuracy to more sophisticated methods of motion-compensation techniques in a fraction of the time and computational burden of those methods, and using far fewer mathematical operations.
The target for the project is CyberKnife (Accuray, Sunnyvale, CA), a frameless robotic radiosurgery system equipped with a small linear particle accelerator and a robotic arm to manipulate the beam. CyberKnife uses real-time respiratory motion compensation system to track patient movement, moving the robotic arm to treat tumors anywhere on the body.
A number of model-based methods are used to predict respiration, including extended Kalman filtering, prediction with fuzzy logic and fuzzy control, sinusoidal models, and others, Ernst explained. The main benefit of prediction is the ability to exploit inherent knowledge about the breathing motion pattern and avoid breakdowns in prediction when unknown data are presented. Still, he said, prediction models can never be perfect, and cannot be made to perform equally well in all patients.
In their study, Ernst and his colleague Dr. Achim Schweikard from the university's Institute for Robotic and Cognitive Systems sought to reduce the computational burden of motion-tracking algorithms while maintaining accuracy.
"It has been observed there is motion both inside and outside due to breathing," Ernst said. "Motion on the inside differs significantly from motion on the outside in direction, amplitude, and phase."
Tracking breathing for a patient with a tumor in the abdomen, for example, involves the attachment of up to 20 light-emitting diodes (LEDs) to the patient's chest and implanting gold fiducial markers around the target tumor to serve as internal landmarks that are visible on imaging. The infrared LEDs are tracked by a stereoscopic infrared camera system, while the landmarks are scanned using stereoscopic x-ray every 30 seconds to one minute, he said.
"What is done next is to build a correlation model that relays the outside motion to the inside motion so that we can interpolate between the x-ray images, which tell us the exact position of the tumor by using the external motion source," Ernst explained.
Following the correlation model, a linear accelerator mounted on a robotic arm is moved to compensate for the breathing-induced motion. This enables the tumor to be irradiated throughout the breathing cycle without the need of fixation, gating, respiratory coaching, or other steps. However, neither the recording of the patient's position nor the repositioning of the robotic system is instantaneous.
"The big problem in this whole situation is that throughout the signaling processing chain we have delays -- delay which comes from acquisition of the data points and delay which comes from the process of computing the correlation model," he said. The algorithm also requires time to compute all the parameters necessary to compensate for breathing motion and the repositioning of the robotic arm, he said.
Unfortunately, current algorithms produce delay as long as 180 msec between the patient's breathing and movement of the CyberKnife's robotic arm, meaning that delays must be compensated for in the model, Ernst said. Even if the delay can be reduced, it cannot be eliminated entirely, so breathing motion must be accurately predicted in advance.
"You cannot move this robot in real-time, so it won't be there when you want it to be where it should be," he said.
To predict breathing, the algorithm must determine the exact system delay -- 120 to 180 msec depending on which generation of the CyberKnife is used -- and predict the future position of the chest LEDs to compensate for the delay. From that the tumor position can be inferred, and the robotic arm aimed at the point where the tumor should be after the delay.
"It's not always perfectly correct, but it's better than doing nothing," Ernst said. And current algorithms are not only slow, but their output can be erratic in certain data environments.
Ernst and Schweikard proposed a new family of multistep linear (MULIN) prediction algorithms based on linear expansions of the prediction error. The simplest form of the algorithm assumes that the difference between the delayed signal and the real signal remains approximately constant over time.
"But this assumption [of constancy] doesn't hold -- the signal does have its peaks and it changes," Ernst said. The researchers accommodated these changes by expanding the prediction error, incorporating higher-order differences in the prediction equation. For this step they introduced a new parameter, l, to control how far back the algorithm should look to determine the change in the signal's first derivative.
"Repeat this over and over again and we arrive at a family of algorithms with a kind of Taylor expansion of the prediction error," he said.
Finally, an exponential smoothing parameter (μ) was introduced to compensate for the inevitable corruption of the signal by noise. Since human breathing does not change abruptly between subsequent sampling points, this parameter helps eliminate rapid changes in the signal, effectively eliminating measurement noise, Ernst said. This step yields the final form of the new multistep linear prediction algorithms.
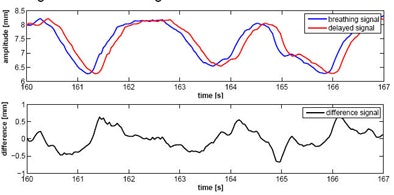 |
| For the simplest form of the MULIN algorithm, Ernst and Schweikard assumed that the difference between the real breathing signal and the delayed signal changes little over time, and that the input signal (y) is equidistantly sampled. (Final versions of the algorithm account for significant changes in the signal.) In the top chart, the blue curve represents the real breathing signal, and the red curve is the signal that is not compensated for the prediction delay. The bottom chart represents the difference between the two signals over time. In the MULIN algorithms, the last available real signal is subtracted from the delayed signal to represent the predicted signal. All images and data courtesy of Floris Ernst. |
 |
 |
 |
MULIN algorithms were used to test several signals, including a "clean artificial signal, the same artificial signal corrupted by Gaussian noise, and, finally, a database of 299 breathing signals (26 Hz sampling rate, 10,000 samples) from patients undergoing radiotherapy treatment at Georgetown University Hospital" in Washington, DC, Ernst said.
The MULIN method was compared to least mean squares-based predictors (LMS) and normalized LMS (nLMS), as well as wavelet-based multiscale autoregression (wLMS), and a multifrequency extended Kalman filter (EKF) approach. Computer-generated data with a prediction horizon of 150 msec were used for testing in the simulation experiments.
In the setting of simulated data without noise, the EKF algorithm outperformed all the other algorithms, but its prediction error increases sharply when even moderate amounts of Gaussian noise were introduced, Ernst said.
On the simulated signal with noise, the MULIN2 algorithm was more accurate than the best other algorithm (nLMS) by 30%. On real data, the MULIN2 algorithm did not equal the accuracy of the best other (wLMS and nLMS), but remained within 3% of their accuracy.
"Our algorithm comes close," Ernst said. "If you have a breathing amplitude of nearly 2 mm, [3%] is negligible because it's in the range of noise," he said.
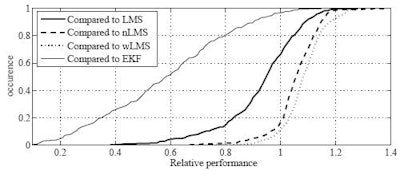 |
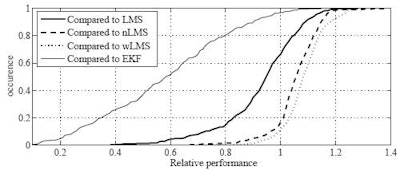
| Cumulative histogram shows relative performance of the best linear predictors compared to LMS, nLMS, wLMS, and EKF prediction. On each of 299 signals from real patient treatments conducted at Georgetown University, the relative normalized (nRMS) error of the best MULIN algorithm was divided by the relative nRMS errors of the LMS, the normalized LMS (nLMS), the wavelet-based multiscale autoregression (wLMS), and the multi-frequency Extended Kalman Filter (EKF) algorithms, respectively. MULIN algorithms outperformed the other algorithms in 66% (LMS), 17% (nLMS), 12% (wLMS), and 97% (EKF) of the test cases. In another 26% (LMS), 54% (nLMS), 47% (wLMS), and 3% (EKF) of the test cases, the best linear algorithm's performance fell short by less than 10%. |
"We have shown that the MULIN algorithms are accurate; they perform as well or nearly as well as the complex algorithms, especially the complex frequency-tracking algorithms, which [MULIN] nearly always outperforms in real settings," Ernst said.
Computational simplicity is the key to its efficiency, he said. MULIN algorithms can predict a signal using fewer than 20 mathematical operations. The more complex EKF and wLMS algorithms require from two and eight full seconds, respectively, to process a signal point representing 30,000 samples -- versus less than 1 msec for MULIN -- an improvement on the order of 10,000, he said.
The speed and simplicity of the algorithms are an important feature that will facilitate their use with a new generation of high-speed tracking systems in development, Ernst said.
"The accuTrack (Atracsys, Botten, Switzerland) tracks motion at 4.1 kH, and [MULIN] would be fast enough to act on signals delivered by the accuTrack in real-time on current normal business PCs," he said.
By Eric Barnes
AuntMinnie.com staff writer
October 10, 2008
Related Reading
PET dose-painting methods produce discordant results, August 27, 2008
Intensity-modulated radiation therapy is inconsistently delivered, March 4, 2008
Lung function guides IMRT planning, October 24, 2007
Linac/MRI prototype allows real-time tumor tracking during rad therapy, September 14, 2007
Cell survival offers IMRT insight on 'bystander effect', November 23, 2007
Copyright © 2008 AuntMinnie.com